Research overview
Non-intrusive model reduction using deep learning
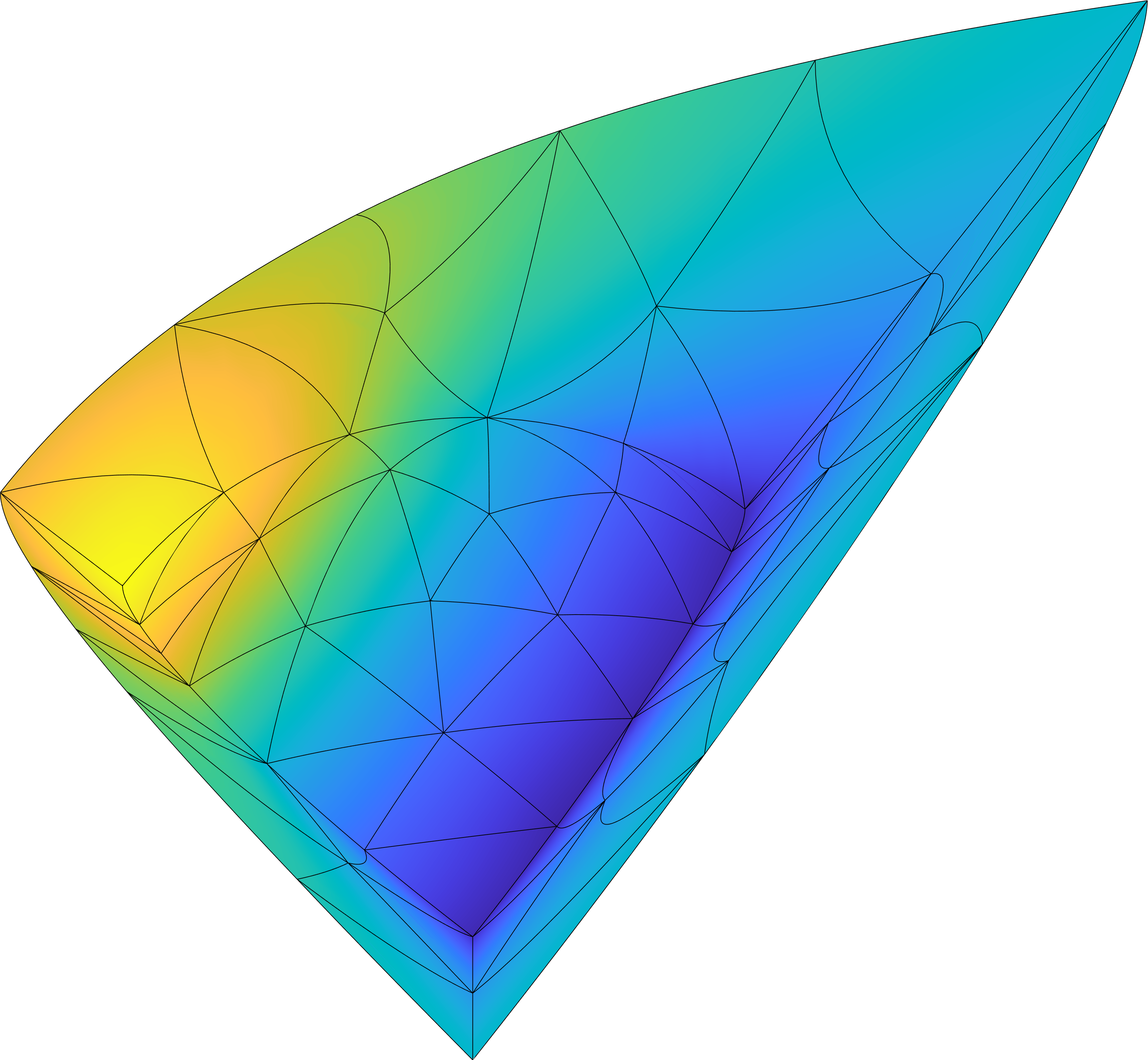
It is well-known that model reduction can only lead to CPU savings for general nonlinear systems if the system reduction is supplemented with an additional step, hyperreduction, to ensure nonlinear terms can be evaluated efficiently. Prevailing methods to approximate the nonlinear terms are code intrusive, potentially requiring years of development time to integrate into an existing codebase, and have been known to lack parametric robustness. We developed a non-intrusive method to efficiently and accurately approximate the expensive nonlinear terms that arise in reduced nonlinear dynamical system using deep neural networks. Once trained, the neural network-based reduced-order model only requires forward and backward propagation through the network to evaluate the nonlinear term and its derivative, which are used to integrate the reduced dynamical system at a new parameter configuration. As such, this method is less code-intrusive than popular hyperreduction approaches, and our numerical experiments also showed it tends to be more stable.
Journal papers
-
H. Gao, J.-X. Wang, and M. J. Zahr, “Non-intrusive model reduction of large-scale, nonlinear dynamical systems using deep learning,” Physica D: Nonlinear Phenomena, vol. 412, p. 132614, 2020. [ bib | DOI | link | arxiv ]
Model reduction with local reduced-order bases
We developed a new approach for dimensionality reduction via projection of nonlinear computational models based on the concept of local reduced-order bases. It is particularly well-suited for problems characterized by different physical regimes or parameter variations. The solution space is partitioned into subregions, and a local reduced-order basis is constructed and assigned to each subregion offline. During the online phase, a local basis is chosen according to the subregion of the solution space where the current high-dimensional solution lies. Low-rank SVD updates are used to efficiently inject online information into reduced-order bases defined offline.
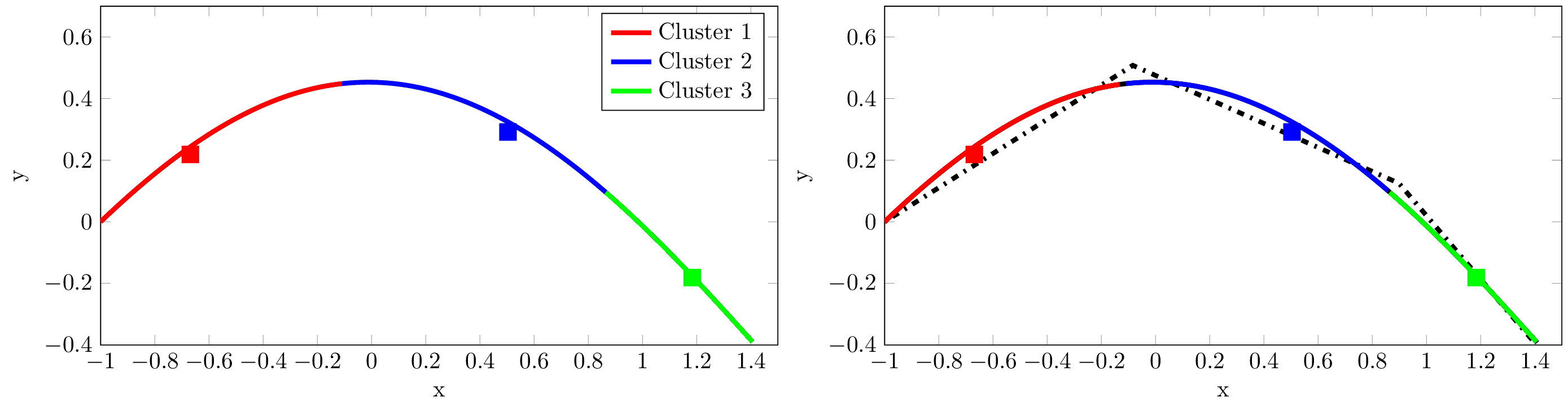
Local model reduction applied to contrived 2D example. Left: Trajectory of the solution and partition in clusters, where the cluster centers are indicated with a square of the appropriate color. Right: Solution of the reduced-order model using 3 local bases of dimension 1.
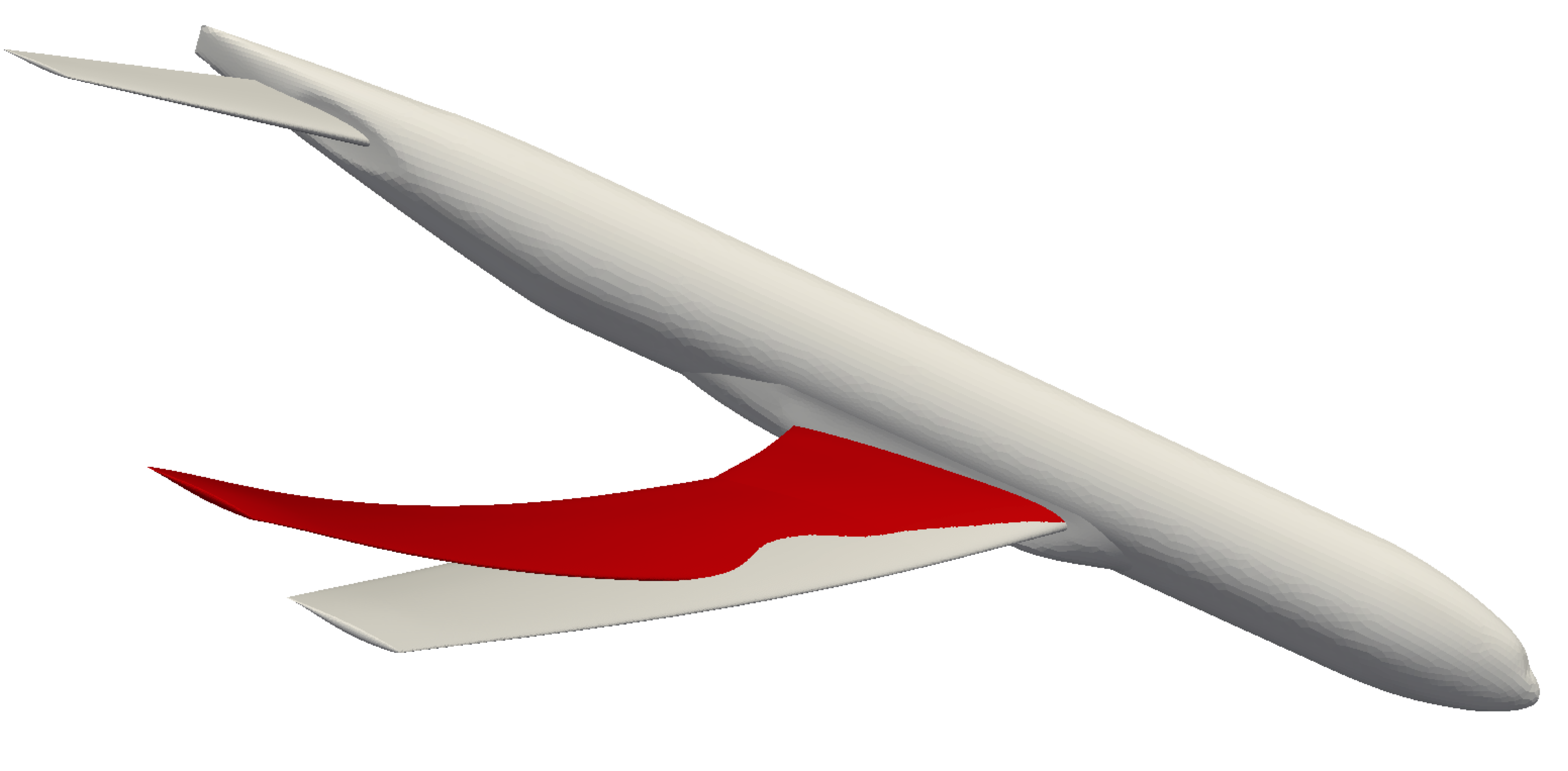
Mesh (left) and pressure (right) of the Ahmed body used to study local model reduction on realistic application.
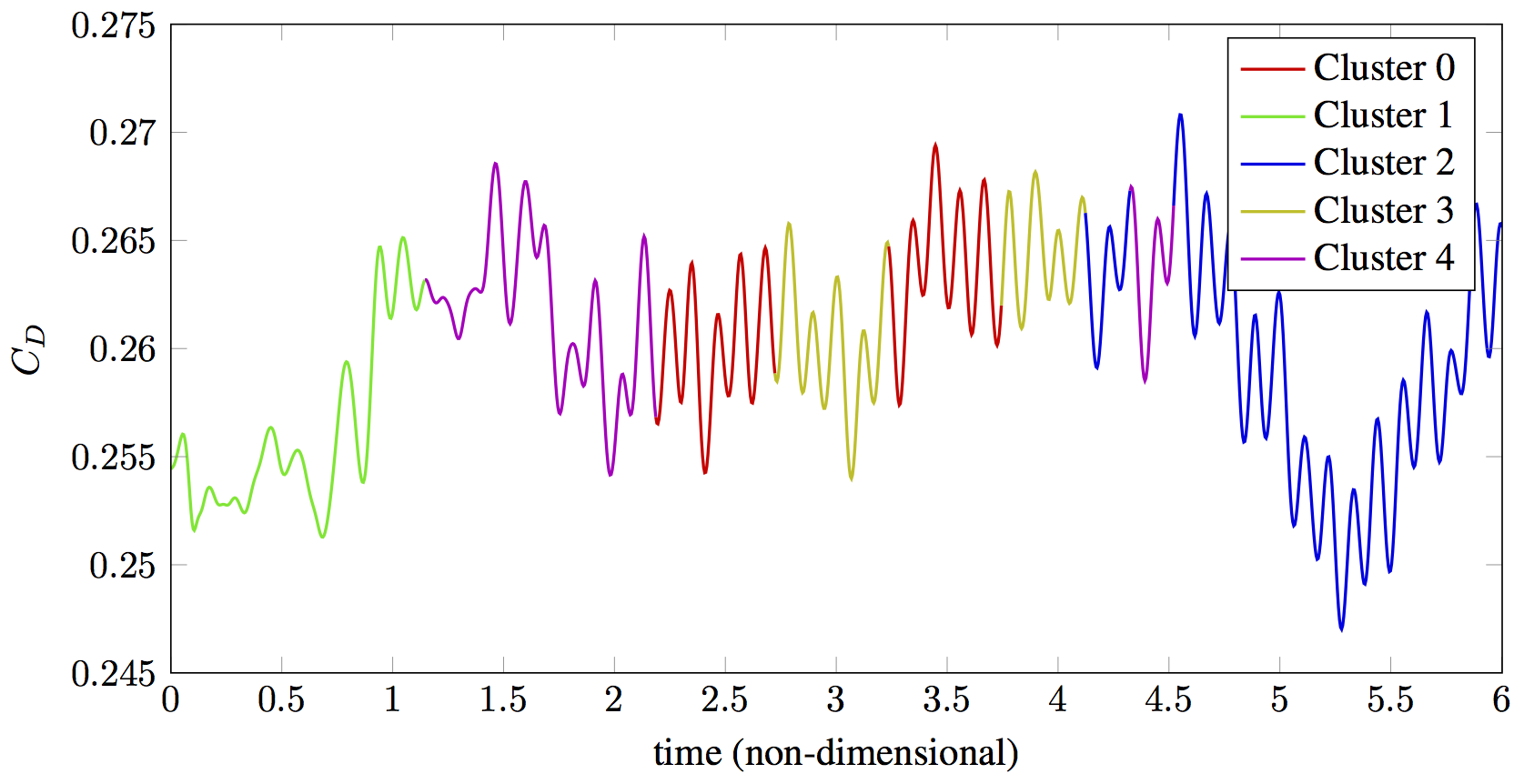
Drag history of the reduced order model using local bases. The color indicates the basis used at a particular time step.
Journal papers
-
D. Amsallem, M. J. Zahr, and K. Washabaugh, “Fast local reduced basis updates for the efficient reduction of nonlinear systems with hyper-reduction,” Advances in Computational Mathematics, pp. 1--44, 2015. [ bib | DOI | link ]
-
D. Amsallem, M. J. Zahr, and C. Farhat, “Nonlinear model order reduction based on local reduced-order bases,” International Journal for Numerical Methods in Engineering, vol. 92, no. 10, pp. 891--916, 2012. [ bib | DOI | link ]
Conference papers
-
K. Washabaugh, M. J. Zahr, and C. Farhat, “On the use of discrete nonlinear reduced-order models for the prediction of steady-state flows past parametrically deformed complex geometries,” in AIAA Science and Technology Forum and Exposition (SciTech 2016), (San Diego, California), American Institute of Aeronautics and Astronautics, AIAA Paper 2016-1814, 1/4/2016 -- 1/8/2016. [ bib | link ]
-
K. Washabaugh, D. Amsallem, M. J. Zahr, and C. Farhat, “Nonlinear model reduction for CFD problems using local reduced-order bases,” in 42nd AIAA Fluid Dynamics Conference and Exhibit, Fluid Dynamics and Co-located Conferences, (New Orleans, Louisiana), American Institute of Aeronautics and Astronautics, AIAA Paper 2012-2686, 6/25/2012 -- 6/28/2012. [ bib | paper | link ]
Talks
-
K. Washabaugh, M. J. Zahr, and C. Farhat, “On the use of discrete nonlinear reduced-order models for the prediction of steady-state flows past parametrically deformed complex geometries,” in AIAA Science and Technology Forum and Exposition (SciTech 2016), (San Diego, California), 1/4/2016 -- 1/8/2016. [ bib ]
-
M. J. Zahr, K. Washabaugh, and C. Farhat, “Robust reduced-order models via fast, low-rank basis updates,” in 2014 SIAM Annual Meeting, (Chicago, Illinois), 7/7/2014 -- 7/11/2014. [ bib | slides ]
-
M. J. Zahr and C. Farhat, “Efficient, parametrically robust nonlinear model reduction using local reduced-order bases,” in 2013 SIAM Conference on Computational Science and Engineering (CSE13), (Boston, Massachusetts), 2/25/2013 -- 3/1/2013. [ bib | slides ]
-
D. Amsallem, K. Washabaugh, M. J. Zahr, and C. Farhat, “Efficient nonlinear model reduction approach using local reduced bases and hyper-reduction,” in 2013 SIAM Conference on Computational Science and Engineering (CSE13), (Boston, Massachusetts), 2/25/2013 -- 3/1/2013. [ bib ]