Computational Mechanics and Optimization Laboratory

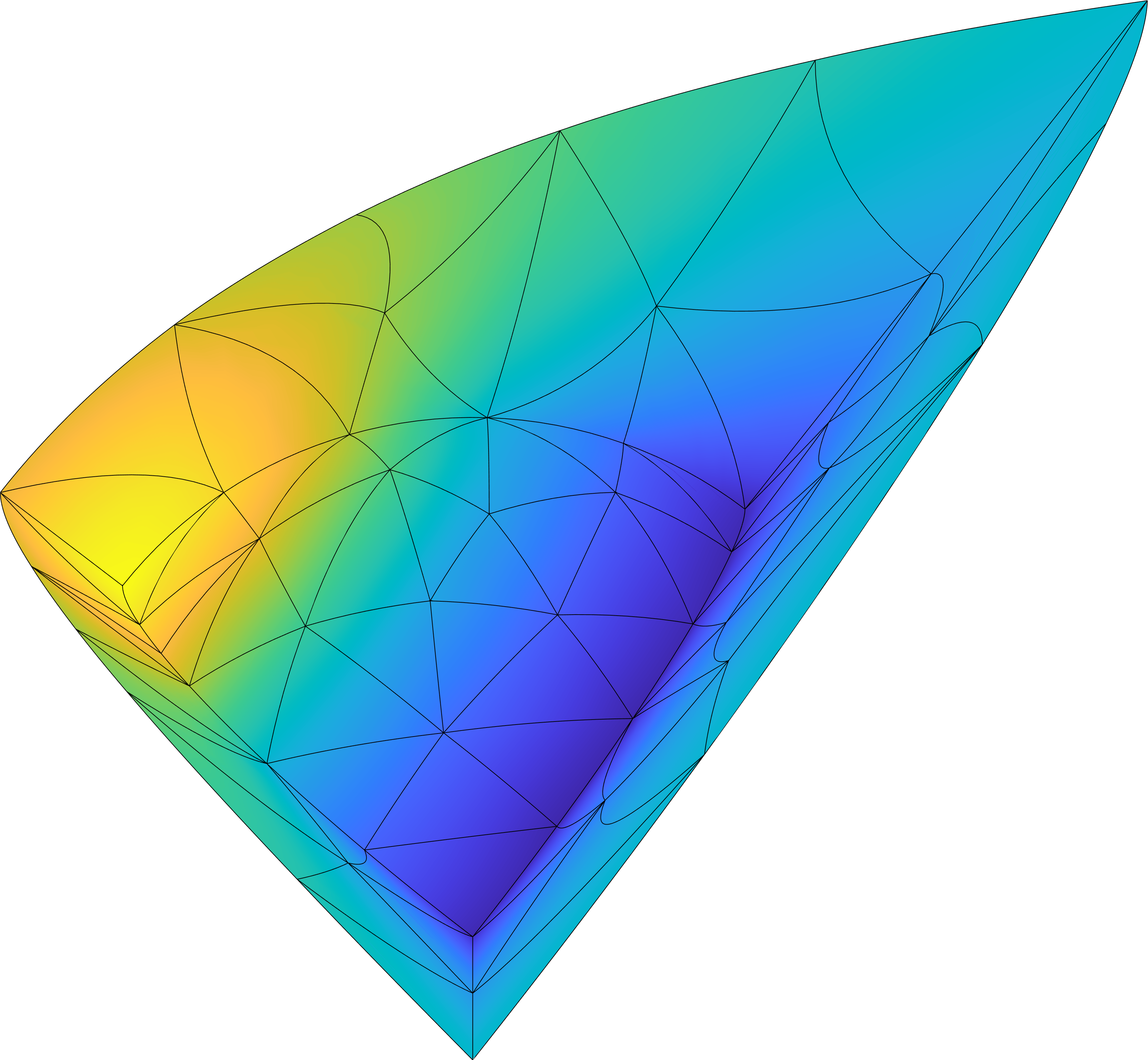
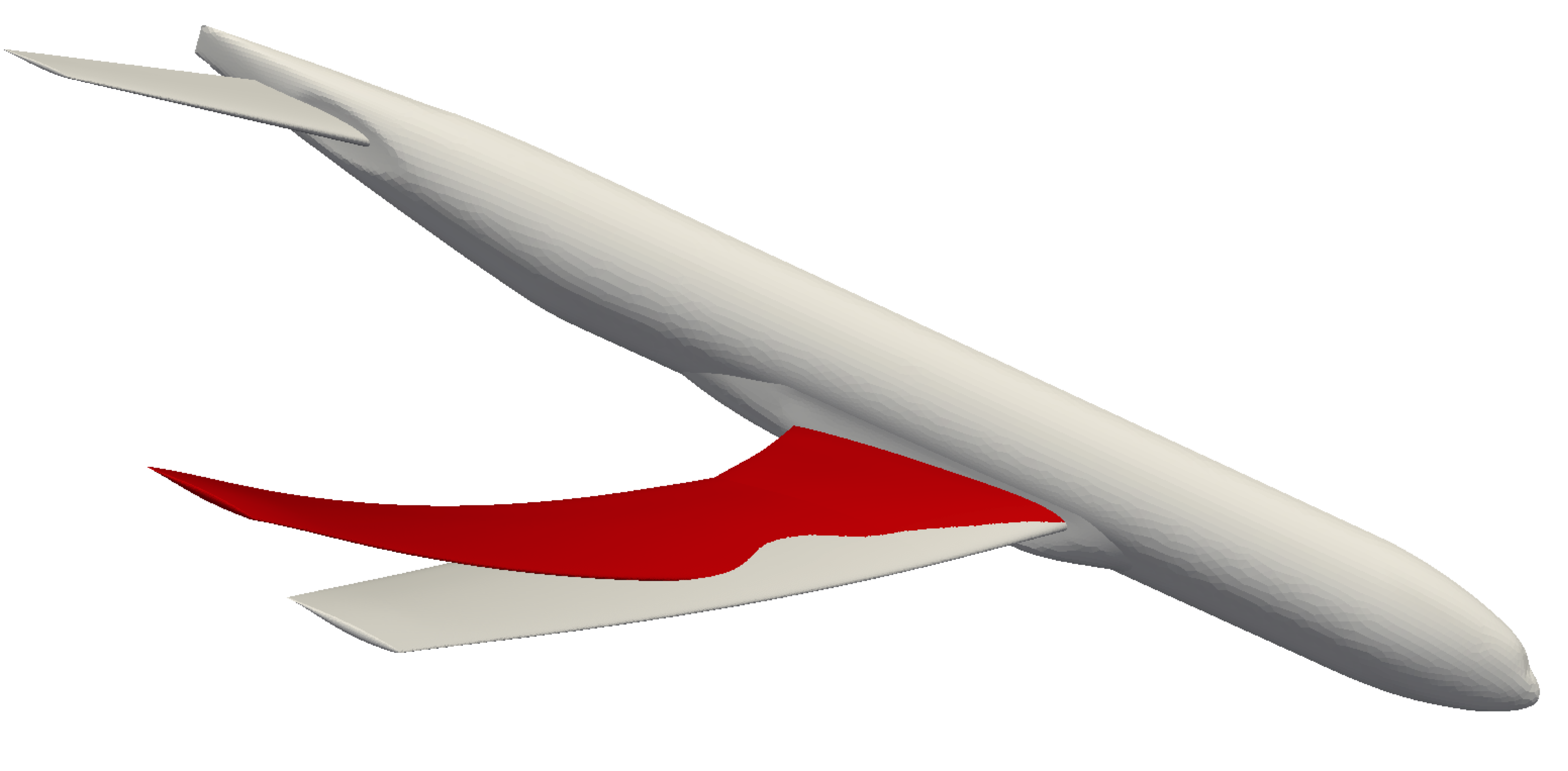
Research overview

High-order implicit shock tracking	Unsteady optimization with high-order discretizations	PDE-constrained optimization using adaptive reduced-order models
Model reduction for multiscale problems	Model reduction methods	Miscellaneous

Time-dependent PDE-constrained optimization with high order methods

Optimization problems constrained by time-dependent Partial Differential Equations (PDEs) commonly arise in engineering practice, particularly in the context of design or control of physics-based systems. We developed and demonstrated a framework for time-dependent PDE-constrained optimization of conservation laws on deforming domains. High-order methods, in both space (discontinuous Galerkin) and time (Runge-Kutta), are used to compute output functionals to high accuracy. The fully discrete sensitivity and adjoint equations were derived and implemented, where special attention was required to properly differentiate the Geometric Conservation Law (GCL) treatment. Applications include optimal control and shape optimization of fluid systems governed by the Navier-Stokes equations.

Time-periodicity constraints

Cyclic steady-state motion of a system, i.e., stable time-periodic behavior, is of central importance in bio-locomotion and many branches of engineering. Examples includef flapping flight, swimming at low or high Reynolds number, helicopter aerodynamics, turbomachinery, wind turbines, and vehicle tires with treads. In this work, we developed a framework for optimizing partial differential equations using gradient-based method on the manifold of time-periodic solutions. We use a Newton-Krylov shooting method with matrix-free GMRES to determine time-periodic flows. We derived and implemented the adjoint equations and method corresponding to the fully discrete, time-periodically constrained PDE. The adjoint equations are linear, two-point boundary value problems that are provably solvable for which we developed a matrix-free GMRES solver with matrix-vector products computed by standard adjoint solves.

Optimization parameters that alter time domain (e.g., frequency)

This work introduces a fully discrete, high-order numerical framework for solving PDE-constrained optimization problems using gradient-based methods in the case where one or more of the optimization parameters affects the time domain; a canonical example being optimization of the frequency of a flapping wing. In a fully discrete setting, this effective parametrization of the time domain leads to a parametrization of the time discretization, e.g., to maintain a fixed number of timesteps per period, the timestep size is parameter-dependent. Gradients of quantities of interest in this work are computed using the adjoint method, which must take into account the parametric dependence of the time discretization.

Application: Superresolution of MR images via PDE-constrained optimization

In collaboration with an MRI research group in Sweden, we have used our time-dependent PDE-constrained optimization methods to superresolve Magnetic Resonsance Images (MRIs), an approach we call Simulation-Based Imaging (SBI). This is a canonical data assimilation problem where we augment our numerical simulations with data to determine appropriate inflow/outflow conditions, which is cast as an optimization problem where we minimize the misfit with the data based on a parametrization of the inflow/outflow velocities.

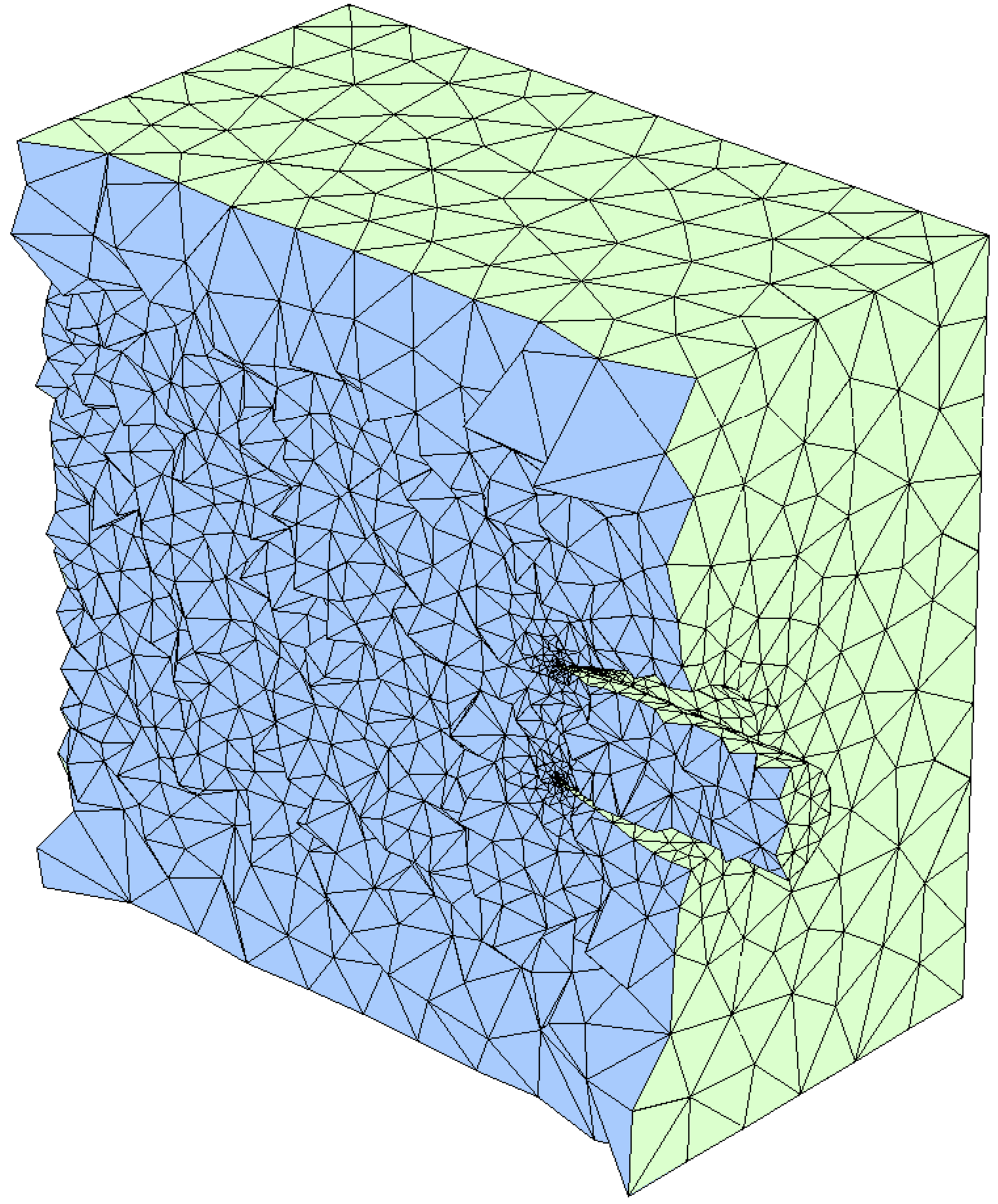
Computational mesh used for MRI data assimilation (left) and reconstructed high-resolution flow (right).

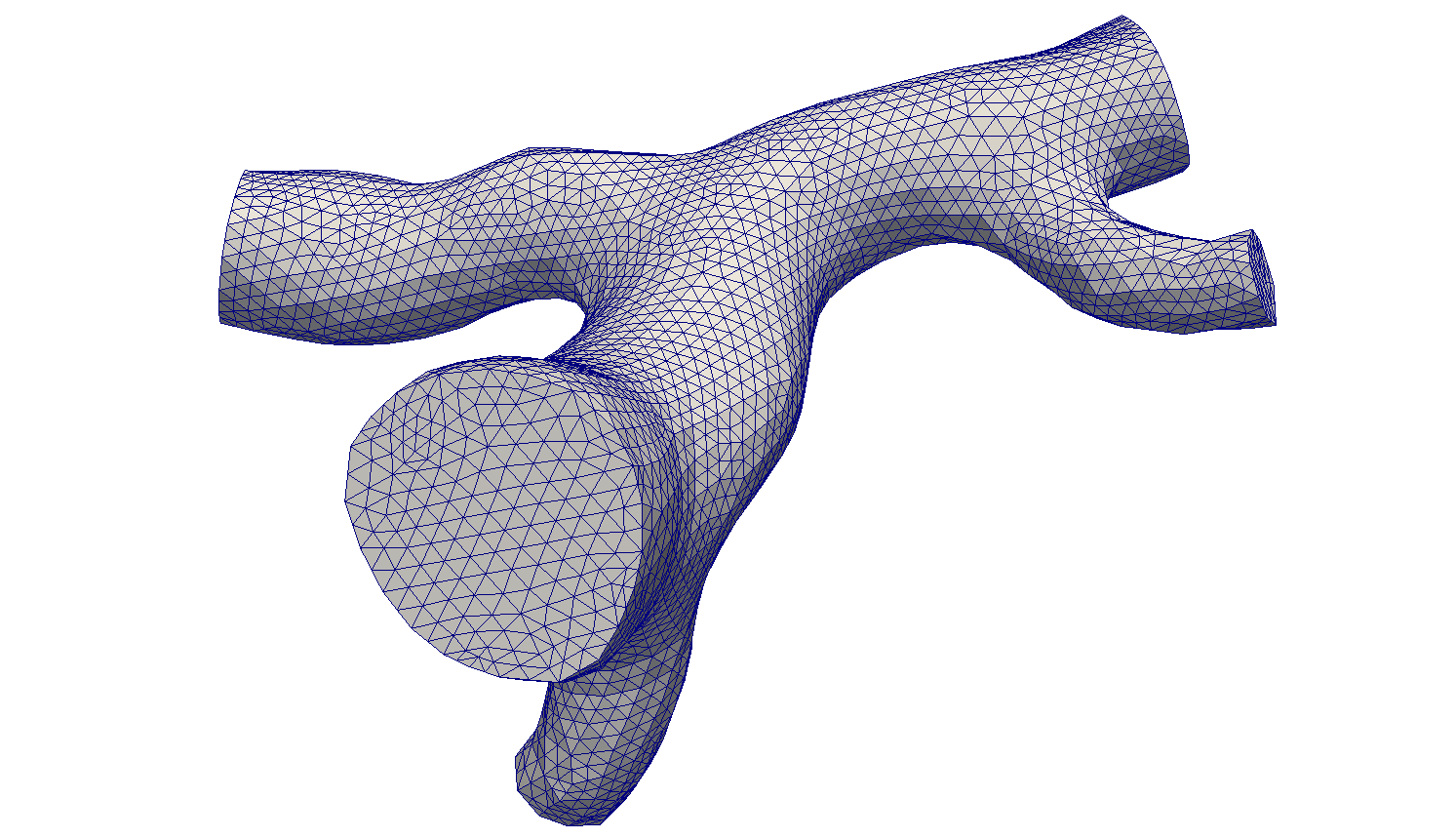
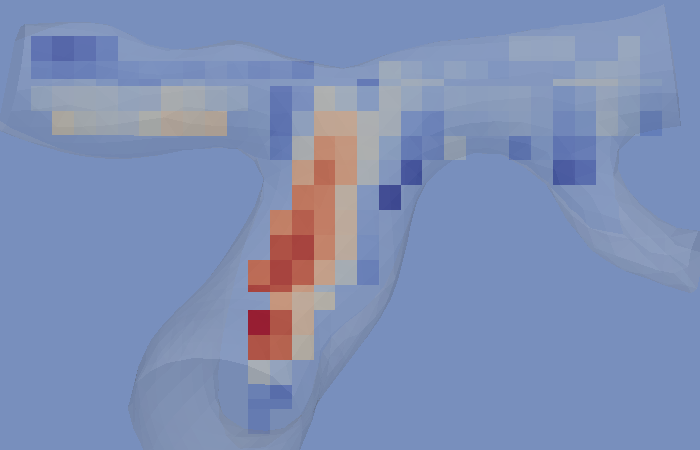
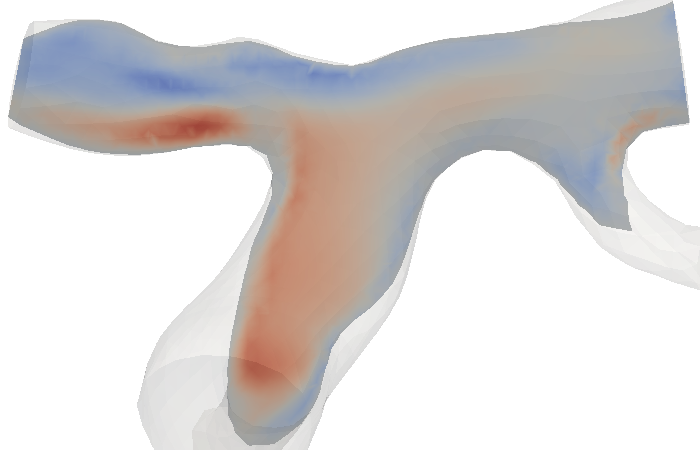
Patient-specific mesh of brain vessel network (Circle of Willis) (left), MRI voxel velocity data on 2D spatial slice at time instance (middle), and SBI reconstruction (right).

Book chapters

• M. J. Zahr and P.-O. Persson, “Energetically optimal flapping wing motions via adjoint-based optimization and high-order discretizations,” in Frontiers in PDE-Constrained Optimization, Springer, 2018. [ bib | paper ]

Journal papers

• C. J. Naudet, J. Töger, and M. J. Zahr, “Accurate quantification of blood flow wall shear stress using simulation-based imaging: a synthetic, comparative study,” Engineering with Computers, pp. 1--17, August 2022. [ bib | DOI | arxiv ]

• J. Töger, M. J. Zahr, N. Aristokleous, K. Markenroth Bloch, M. Carlsson, and P.-O. Persson, “Blood flow imaging by optimal matching of computational fluid dynamics to 4D flow data,” Magnetic Resonance in Medicine, vol. 84, no. 4, pp. 2231--2245, 2020. [ bib | DOI | link ]

• M. J. Zahr and P.-O. Persson, “An adjoint method for a high-order discretization of deforming domain conservation laws for optimization of flow problems,” Journal of Computational Physics, vol. 326, pp. 516 -- 543, 2016. [ bib | DOI | arxiv | link ]

• M. J. Zahr, P.-O. Persson, and J. Wilkening, “A fully discrete adjoint method for optimization of flow problems on deforming domains with time-periodicity constraints,” Computers & Fluids, vol. 139, pp. 130 -- 147, 2016. [ bib | DOI | arxiv | link ]

Conference papers

• J. Wang, M. J. Zahr, and P.-O. Persson, “Energetically optimal flapping flight based on a fully discrete adjoint method with explicit treatment of flapping frequency,” in 23rd AIAA Computational Fluid Dynamics Conference, (Denver, Colorado), American Institute of Aeronautics and Astronautics, AIAA Paper 2017-4412, 6/5/2017 -- 6/9/2017. [ bib | paper | link ]

• M. J. Zahr and P.-O. Persson, “High-order, time-dependent aerodynamic optimization using a discontinuous Galerkin discretization of the Navier-Stokes equations,” in AIAA Science and Technology Forum and Exposition (SciTech 2016), (San Diego, California), American Institute of Aeronautics and Astronautics, AIAA Paper 2016-0064, 1/4/2016 -- 1/8/2016. [ bib | paper | link ]

Talks

• C. Naudet and M. J. Zahr, “Predicting wall shear stress using simulation-based imaging,” in 16th U.S. National Congress on Computational Mechanics (USNCCM16), (Chicago, Illinois), 7/25/2021 -- 7/29/2021. [ bib ]

• M. J. Zahr, “Integrating computational physics and numerical optimization to address challenges in computational science, engineering, and medicine,” in Applied and Computational Mathematics and Statistics Seminar, University of Notre Dame (Host: Alan Lindsay), (Virtual Event; Notre Dame, Indiana), University of Notre Dame, 4/8/2021. [ bib | slides ]

• M. J. Zahr, “High-resolution visualization of in vivo blood flow from low-resolution 4D flow MRI scans using computational fluid dynamics and optimization,” in SIAM Conference on Parallel Processing for Scientific Computing (PP20), (Seattle, Washington), 2/12/2020 -- 2/15/2020. [ bib ]

• M. J. Zahr, “Integrating computational physics and numerical optimization to address challenges in computational science, engineering, and medicine,” in Data Sciences Seminar, Johns Hopkins University (Host: Fei Lu), (Baltimore, Maryland), Johns Hopkins University, 12/4/2019. [ bib ]

• M. J. Zahr, “Integrated computational physics and numerical optimization,” in Center for Informatics and Computational Science Seminar, Univerity of Notre Dame (Host: Nicholas Zabaras), (Notre Dame, Indiana), University of Notre Dame, 3/6/2019. [ bib ]

• M. Franco, P.-O. Persson, W. Pazner, and M. J. Zahr, “An adjoint method using fully implicit Runge-Kutta schemes for optimization of flow problems,” in AIAA Science and Technology Forum and Exposition (SciTech2019), (San Diego, California), 1/7/2019 -- 1/11/2019. [ bib ]

• M. J. Zahr, “Integrated computational physics and numerical optimization,” in Program in Applied Mathematics Colloquium, University of Arizona (Host: Matthias Morzfeld), (Tuscon, Arizona), University of Arizona, 9/21/2018. [ bib | slides ]

• M. J. Zahr, “Integrated computational physics and numerical optimization,” in Applied Mathematics Seminar, UC Berkeley (Host: Per-Olof Persson), (Berkeley, California), University of California, Berkeley, 9/6/2018. [ bib | slides ]

• M. J. Zahr, “Optimization-based computational physics and high-order methods: from optimized analysis to design and data assimilation,” in Aerospace and Ocean Engineering Seminar, Virginia Tech (Host: Kevin Wang), (Blacksburg, Virginia), Virginia Polytechnic Institute and State University, 4/2/2018. [ bib ]

• M. J. Zahr, “Optimization-based computational physics and high-order methods: from optimized analysis to design and data assimilation,” in LBNL CRD Postdoc Seminar Series, (Berkeley, California), Lawrence Berkeley National Laboratory, 9/18/2017. [ bib | slides ]

• J. Wang, M. J. Zahr, and P.-O. Persson, “Energetically optimal flapping flight based on a fully discrete adjoint method with explicit treatment of flapping frequency,” in 23rd AIAA Computational Fluid Dynamics Conference, (Denver, Colorado), 6/5/2017 -- 6/9/2017. [ bib | slides ]

• M. J. Zahr, “Gradient-based optimization of flow problems using the adjoint method and high-order numerical discretizations,” in Applied, Computational, and Industrial Math Seminar Series, (San Jose, California), San Jose State University, 5/8/2017. [ bib | slides ]

• M. J. Zahr, “Adjoint-based PDE-constrained optimization using globally high-order numerical discretizations,” in 2017 Berkeley/Stanford Computational Mechanics Festival (CompFest), (Berkeley, California), University of California, Berkeley, 5/8/2017. [ bib | slides ]

• M. J. Zahr and P.-O. Persson, “Optimization of CFD simulations, with MRI applications,” in TESLA Seminar (Host: Johannes Töger), (Lund, Sweden), Lund University, 3/31/2017. [ bib | slides ]

• M. J. Zahr and P.-O. Persson, “High-order, time-dependent aerodynamic optimization using a discontinuous Galerkin discretization of the Navier-Stokes equations,” in AIAA Science and Technology Forum and Exposition (SciTech 2016), (San Diego, California), 1/4/2016 -- 1/8/2016. [ bib | slides | paper ]

• M. J. Zahr and P.-O. Persson, “High-order methods for optimization and control of conservation laws on deforming domains,” in Dean Seminar at Sandia National Laboratories (Host: Kevin Carlberg), (Livermore, California), 12/14/2015. [ bib | slides ]

• M. J. Zahr and P.-O. Persson, “High-order methods for optimization and control of conservation laws on deforming domains,” in Applied Mathematics Seminar at UC Berkeley (Host: Per-Olof Persson), (Berkeley, California), 9/30/2015. [ bib | slides ]

• M. J. Zahr, “High-order, time-dependent PDE-constrained optimization using discontinuous Galerkin methods,” in Department of Energy Computational Science Graduate Fellowship Program Review, (Washington D.C.), 7/27/2015 -- 7/30/2015. [ bib | slides ]

• M. J. Zahr and P.-O. Persson, “Unsteady CFD optimization using high-order discontinuous Galerkin finite element methods,” in 13th U.S. National Congress on Computational Mechanics (USNCCM13), (San Diego, California), 7/26/2015 -- 7/30/2015. [ bib | slides ]

Posters

• M. J. Zahr and P.-O. Persson, “Adjoint-based optimization, uncertainty quantification, and data assimilation of multiphysics systems using high-order numerical discretizations,” in DOE ASCR Applied Mathematics PI Meeting, (Washington D.C.), 9/11/2017 -- 9/12/2017. [ bib | poster ]

• M. J. Zahr and P.-O. Persson, “Unsteady PDE-constrained optimization using high-order DG-FEM,” in 13th U.S. National Congress on Computational Mechanics (USNCCM13), (San Diego, California), 7/26/2015 -- 7/30/2015. [ bib | poster ]